Target Sum 是在练习递归算法（回溯算法）时遇到的经典题目。从无优化的回溯到加上备忘录的回溯，再到动态规划算法，其中步步优化的思想至关重要。

问题描述

You are given a list of non-negative integers, a1, a2, …, an, and a target, S. Now you have 2 symbols + and -. For each integer, you should choose one from + and - as its new symbol.

Find out how many ways to assign symbols to make sum of integers equal to target S.

Example 1:

Input: nums is [1, 1, 1, 1, 1], S is 3. 
Output: 5
Explanation: 

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

Note:

The length of the given array is positive and will not exceed 20.
The sum of elements in the given array will not exceed 1000.
Your output answer is guaranteed to be fitted in a 32-bit integer.

解法

1 Brute Force

我们将最常规的回溯算法称为 Brute Force，即尝试在当前位置分别放上“+”和“-”，计算当前（新的）和，并调用自身。当每个数字前的符号都已确定（迭代步数达到最大）时，计数器加一。这是经典的回溯算法，时间复杂度是 $O(2^n)$，空间复杂度度是 $O(n)$，表示递归树的深度。

public class Solution {
    int count = 0;
    public int findTargetSumWays(int[] nums, int S) {
        calculate(nums, 0, 0, S);
        return count;
    }
    public void calculate(int[] nums, int i, int sum, int S) {
        if (i == nums.length) {
            if (sum == S)
                count++;
        } else {
            calculate(nums, i + 1, sum + nums[i], S);
            calculate(nums, i + 1, sum - nums[i], S);
        }
    }
}

2 带备忘录的递归

注意到，上述简单粗暴的直接回溯面临许多重复计算：当迭代步数与当前数字和都一致时。下图可以帮助理解这一重复计算发生的情况，我们以题目给的例子为例，其中紫色标号为「当前步数的数字和」，圈出来的部分是等效的只需计算一次。

重复计算

我们使用一个新数组作为备忘录，该数组应为二维，因为备忘录的索引需要由「迭代步」和「当前数字和」两个元素来确定。每次调用 calculate(nums, i, sum, S) 时，我们将其返回的结果（该情况下的满足条件的路径数目）保存到 memo[i][sum+1000] 中，1000 是为了使索引都为正数。使用备忘录的算法时间复杂度为 $O(l \times n)$，其中 $l$ 为 sum 的范围。

public class Solution {
    int count = 0;
    public int findTargetSumWays(int[] nums, int S) {
        int[][] memo = new int[nums.length][2001];
        for (int[] row: memo)
            Arrays.fill(row, Integer.MIN_VALUE);
        return calculate(nums, 0, 0, S, memo);
    }
    public int calculate(int[] nums, int i, int sum, int S, int[][] memo) {
        if (i == nums.length) {
            if (sum == S)
                return 1;
            else
                return 0;
        } else {
            if (memo[i][sum + 1000] != Integer.MIN_VALUE) {
                return memo[i][sum + 1000];
            }
            int add = calculate(nums, i + 1, sum + nums[i], S, memo);
            int subtract = calculate(nums, i + 1, sum - nums[i], S, memo);
            memo[i][sum + 1000] = add + subtract;
            return memo[i][sum + 1000];
        }
    }
}

## 3 二维动态规划

考虑常规递归方法的时间复杂度 $O(2^n)$。事实上，所有可能的 sum 只有 2001 种情形（在此题的要求下）。动态规划也常用于计数问题，比起指数级时间复杂度，其优势明显。

在该问题的动态规划方法中，用 dp[i][j] 表示使用 nums[0..i] 可以计算出和 j。那么可否由 dp 中第 i 行所有可能的 sum （即可取的那些 j）来确定 i+1 行可取 sum 的可能情况数？首先，记「用 nums[0..i] 可以表示出的所有sum」为数字集合 $V_i$，那么 $ V_{i+1} = \{ V_{i} + num_i \} \cup \{ V_{i} - num_i \} $。对于 dp[i + 1][j]，可由公式 dp[i + 1][j] = dp[i][j - nums[i]] + dp[i][j + nums[i]] 算得。

花花酱的博文对这一过程的动态规划原理做了深入解析。注意图中两种不同的状态转移方程是等价的。

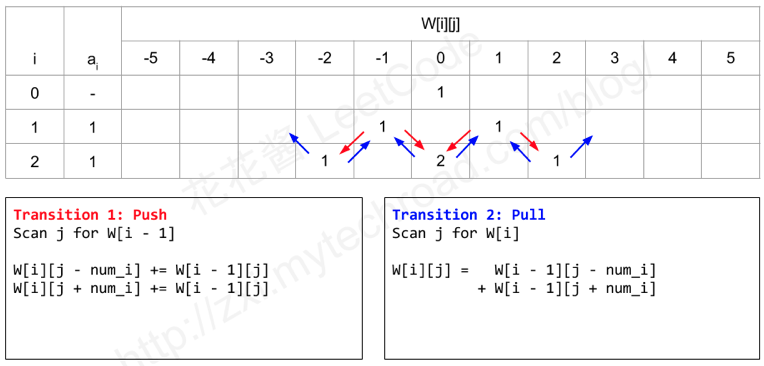
填值过程如下图所示。所求结果在表格的最后一行。

二维动态规划算法代码如下。时间复杂度是 $O(l \times n)$，其中 $l$ 代表可能算术和的范围跨度，这里是个常数 2001；$n$ 是 nums 中数字个数。空间复杂度是 $O(l \times n)$。

public class Solution {
    public int findTargetSumWays(int[] nums, int S) {
        int[][] dp = new int[nums.length][2001];
        dp[0][nums[0] + 1000] = 1;
        dp[0][-nums[0] + 1000] += 1;
        for (int i = 1; i < nums.length; i++) {
            for (int sum = -1000; sum <= 1000; sum++) {
                if (dp[i - 1][sum + 1000] > 0) {
                    dp[i][sum + nums[i] + 1000] += dp[i - 1][sum + 1000];
                    dp[i][sum - nums[i] + 1000] += dp[i - 1][sum + 1000];
                }
            }
        }
        return S > 1000 ? 0 : dp[nums.length - 1][S + 1000];
    }
}

4 一维动态规划

可见，二维动态规划方法中，在计算 dp 二维数组的每一行时，只需要上一行，上一行以上的数据都已不再需要，因此可用滚动数组的方法将其降为到一维数组。这样，dp 一维数组在每个迭代步骤时都被修改。

public class Solution {
    public int findTargetSumWays(int[] nums, int S) {
        int[] dp = new int[2001];
        dp[nums[0] + 1000] = 1;
        dp[-nums[0] + 1000] += 1;
        for (int i = 1; i < nums.length; i++) {
            int[] next = new int[2001];
            for (int sum = -1000; sum <= 1000; sum++) {
                if (dp[sum + 1000] > 0) {
                    next[sum + nums[i] + 1000] += dp[sum + 1000];
                    next[sum - nums[i] + 1000] += dp[sum + 1000];
                }
            }
            dp = next;
        }
        return S > 1000 ? 0 : dp[S + 1000];
    }
}