[LC33-35] Search in Array / 二分查找法

发表于 | 分类于 ，

本篇探讨二分查找法在数组检索中的应用。

33 Search in Rotated Sorted Array

Search in Rotated Sorted Array - LeetCode

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.
(i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2).
You are given a target value to search. If found in the array return its index, otherwise return -1.
You may assume no duplicate exists in the array.

这道搜索问题直接求解的话思路应该是：先用 O(n) 时间复杂度的遍历找到 转折点，然后两边分别应用二分查找法。这样，算法复杂度是 O(n)，而二分查找法 O(log n) 的优势没有发挥出来。

变换后数组的特点

以有序数列 0 1 2 4 5 6 7 为例，经过变换后可能得到 4 5 6 7 0 1 2。

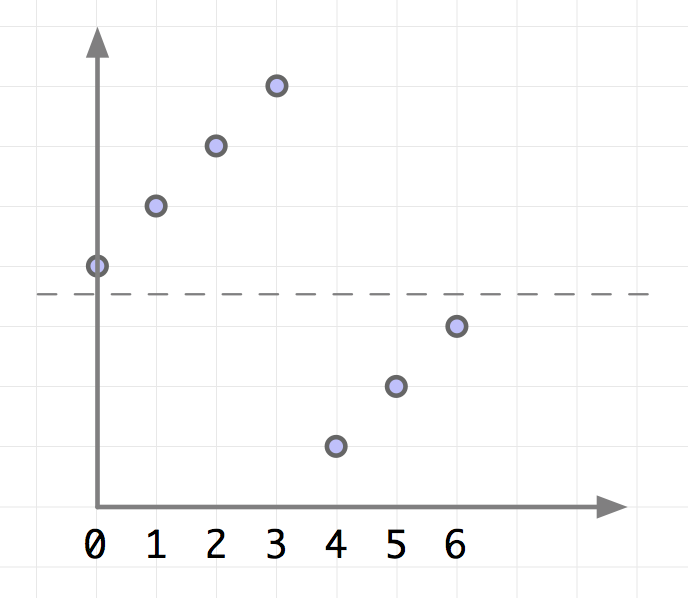
图中可以看出，无论转折点在哪里，前一部分的任意元素都大于后一部分的任意元素。

二分法的关键：哪一边。

仅运用一次二分查找法的方法是：每次确定中间元素后，判断 s[start...mid] 和 s[mid...end] 何者为有序的，这样就能进一步确定 target 处于两者中的哪一段。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class Solution {
    public int search(int[] nums, int target) {
        int start = 0;
        int end = nums.length - 1;
        while (start <= end){
            int mid = (start + end) / 2;
            if (nums[mid] == target)
                return mid;

            if (nums[start] <= nums[mid]){
                 if (target < nums[mid] && target >= nums[start])
                    end = mid - 1;
                 else
                    start = mid + 1;
            }

            if (nums[mid] <= nums[end]){
                if (target > nums[mid] && target <= nums[end])
                    start = mid + 1;
                 else
                    end = mid - 1;
            }
        }
        return -1;
    }
}

一种更简单的方法

另一种方法对二分查找法稍作修改，根据最小元素所在位置（转折点）在每次进行 target 与 中值 比较时用 数组原始序中该位置的值 进行比较（给 mid 加上一个偏移）。有点绕😵。

在第2步中，留意到：二分查找法的关键因素只有首尾索引值和中值及其索引值，其他位置上的值是不相关的。

方法思路是：

  1. 先用二分查找法找到最小元素（即转折点）。

    1
    2
    3
    4
    5
    6
    int lo = 0, hi = n - 1;
    while(lo < hi){
        int mid = (lo + hi) / 2;
        if(A[mid] > A[hi]) lo = mid + 1;
        else hi = mid;
    }

  2. 用（修改的）二分查找法确定位置。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    int rot = lo;
    lo = 0; hi = n - 1;
    while(lo <= hi){
        int mid = (lo + hi) / 2;
        int realmid = (mid + rot) % n;
        if(A[realmid] == target) return realmid;
        if(A[realmid] < target) lo = mid + 1;
        else hi = mid - 1;
    }
    return -1;

还有一种以上方法的修改版本：确定转折点后，确定 target 在转折点的左侧或右侧，只在一侧进行二分查找。

34 Search for a Range

Search for a Range

Given an array of integers sorted in ascending order, find the starting and ending position of a given target value.
Your algorithm’s runtime complexity must be in the order of O(log n).
If the target is not found in the array, return [-1, -1].
For example, given [5, 7, 7, 8, 8, 10] and target value 8, return [3, 4].

两次使用二分法和分类讨论

为了求得一个起止范围，将起点和终点分别用一次二分法求出。

以二分法求解「起始点」为例说明。初始化两个指针为i = 0和j = n - 1。每个迭代步骤计算中值mid = (i + j) / 2，并比较A[mid]和target的大小：

  1. 如果A[mid] < target，那么所求范围的起始点必定在mid的 右边（下一个迭代步骤中i = mid + 1）；
  2. 如果A[mid] > target，那么所求范围的起始点必定在mid的 左边（j = mid - 1）；
  3. 如果A[mid] == target，那么所求范围的起始点必定在mid的 左边 或者 正好在mid处（j = mid）。

2、3两种情况都视为将右侧指针左移，即

  • 如果A[mid] >= target，那么j = mid。

将这些条件语句放到二分法的循环主体 while (i < j) 中，当循环结束时，i或j均指向 所求范围的起始点。注意：在每一个迭代步骤，范围都进一步缩小（而不能陷入死循环）。

为什么i或j均指向起始点？考虑以下几种情况（多次迭代后最终都将只剩两个元素，假设target = 5）：

1
2
3
4
5
6
7
case 1: [5 7] (A[i] = target < A[j])
case 2: [5 3] (A[i] = target > A[j])
case 3: [5 5] (A[i] = target = A[j])
case 4: [3 5] (A[j] = target > A[i])
case 5: [3 7] (A[i] < target < A[j])
case 6: [3 4] (A[i] < A[j] < target)
case 7: [6 7] (target < A[i] < A[j])

1、2、3三种情况中，都将执行j = mid，从而j也将指向前一个元素；第4种情况中，将会执行i = mid+1，结果成立；其他情况中，5不在序列中，且A[i] != target。

因此，算法最后需要判定：如果A[i] == target，那么i为起始点；否则，返回-1。

范围要不断缩小

下面考虑「结束点」的求解。与上述过程类似，但方向相反。可以得出结论：

  1. 如果A[mid] > target，那么j = mid - 1；
  2. 如果A[mid] <= target，那么i = mid。

然而，这引发了一个「死循环」，例如，当 [5 7], target = 5 时，赋值语句i = mid不起作用，范围不再收缩。

解决方法是微调 mid 的赋值语句（额外加1），使得每次计算中值 往右取整，即：mid = (i + j) / 2 + 1。这样，我们能够在每一次迭代时，进一步收缩范围（每次通过i = mid设置i的新值时都能 使其改变）。同样地，考虑计算「起始点」的过程，每次通过j = mid设置j的新值时，j必定发生变化使范围缩小。这就是为mid额外加1的目的。

具体步骤及代码参考 帖子。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
vector<int> searchRange(int A[], int n, int target) {
    int i = 0, j = n - 1;
    vector<int> ret(2, -1);
    // Search for the left one
    while (i < j)
    {
        int mid = (i + j) /2;
        if (A[mid] < target) i = mid + 1;
        else j = mid;
    }
    if (A[i]!=target) return ret;
    else ret[0] = i;
    
    // Search for the right one
    j = n-1;  // We don't have to set i to 0 the second time.
    while (i < j)
    {
        int mid = (i + j) /2 + 1;	// Make mid biased to the right
        if (A[mid] > target) j = mid - 1;  
        else i = mid;				// So that this won't make the search range stuck.
    }
    ret[1] = j;
    return ret; 
}

35 Search Insert Position

问题 Search Insert Position 描述了「在有序数组中插入一个整数，输出其在插入该值后（形成的有序）数组中的位置」。

很容易想到用二分法确定位置。值得一提的是编写（二分法）代码时有两个关键点需要注意，这在上面两个问题中也有讨论。

  1. 确定 end 是 nums.length 还是 nums.length - 1。
  2. 由于mid = (beg + end) / 2，因此 beg <= mid, mid < end。于是，beg = mid + 1 使 beg 总能增加；end = mid 使 hi 总能减少。（向左取整）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public int searchInsert(int[] nums, int target) {
    int n = nums.length;
    int beg = 0, end = n - 1;
    while (beg <= end) {
        int mid = beg + (end - beg) / 2;
        if (target == nums[mid]) return mid;
        else if (target < nums[mid]) {
            end = mid - 1;
        } else {
            beg = mid + 1;
        }
    }
    return beg;
}

上述算法将两种情况合并处理（不是通常的二分法）。其中修改了 while 语句的条件，并且 target 找到的情况直接返回。如果 target 不在序列中，则 beg == end 成立并且继续进入循环中，根据 target 与 nums[beg] 的大小情况减小 end 或增加 beg，在下一次退出循环，并返回原先的 beg 或增加 1 后的 beg。