[LC31] Next Permutation / 排列

与排列数有关的问题（计算所有排列的递归方法和非递归方法）。

Implement next permutation, which rearranges numbers into the lexicographically next greater permutation of numbers.
If such arrangement is not possible, it must rearrange it as the lowest possible order (ie, sorted in ascending order).
The replacement must be in-place and use only constant extra memory.
Here are some examples. Inputs are in the left-hand column and its corresponding outputs are in the right-hand column.
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1

如果使用 Brute Force 方法，穷举字符串所有排列将带来 $O(n!)$ 的时间复杂度和 $O(n)$ 的空间复杂度。开销较大，考虑用更为简单的方法实现。

如何求解一组数字的所有排列？本篇介绍解决这一问题的递归方法和非递归方法。其中，非递归方法每个迭代步骤计算下一个排列数。本题是这一大问题的一部分。

问题：求解数组的所有排列

递归方法

以字符串 abc 为例，其所有排列（按字典序）是：

abc、acb
bac、bca
cab、cba

如果暴力穷举则会带来 $O(n^n)$ 的时间复杂度。

考虑 bac 和 cba 这两个字符串。两者都是由 abc 中的 a 与后面两字符交换得到的。然后将 abc 的第 2 个字符和第 3 个字符交换得到 acb。同理再由 bac 和 cba 得到 bca 和 cab。

由此可见，全排列的实现方式是：分别将当前字符串每个位置与首字符交换，求首字符位置以外剩余部分的全排列。以此实现递归。注意，这样计算的结果列表中每个字符串不是按照字典序排列的。

//递归全排列，start 为全排列开始的下标， length 为str数组的长度
void AllRange(char* str, int start, int length) {
	if(start == length-1) {
		printf("%s\n", str);
	}
	else {
		for(int i = start; i <= length-1; i++) {
            //从下标为start的数开始，分别与它后面的数字交换
			Swap(&str[start], &str[i]); 
			AllRange(str, start+1, length);
			Swap(&str[start], &str[i]); 
		}
	}
}
void Permutation(char* str) {
	if(str == NULL) return;
	AllRange(str, 0, strlen(str));
}

递归方法的时间复杂度和空间复杂度均为 $O(n!)$，效率很低。

处理重复元素

如果出现重复元素，需要对上述算法略做改动。

考虑输入 abb。由于 abb 能得到 bab 和 bba，而 bab 又可得到 bba，是否可以考虑不计算由 abb 变换而得的 bba？第一个字符 a 与第二个字符 b 交换得到 bab，然后考虑第一个字符 a 与第三个字符 b 交换，此时由于第三个字符等于第二个字符，所以它们不再交换。再考虑 bab，它的第二个与第三个字符交换可以得到 bba。此时全排列生成完毕，即 abb、bab 和 bba。

处理重复元素的规则是：从当前字符串的第一个元素起分别与其后非重复出现的元素交换。

//在 str 数组中，[start,end) 中是否有与 str[end] 元素相同的
bool IsSwap(char* str, int start, int end) {
	for(; start<end; start++) {
		if(str[start] == str[end])
			return false;
	}
	return true;
}
//递归去重全排列，start 为全排列开始的下标， length 为str数组的长度
void AllRange2(char* str, int start, nt length) {
	if (start == length-1) {
		printf("%s\n", str);
	}
	else {
		for (int i = start; i <= length-1; i++) {
			if (IsSwap(str, start, i)) {
				Swap(&str[start], &str[i]); 
				AllRange2(str, start+1, length);
				Swap(&str[start], &str[i]); 
			}
		}
	}
}
void Permutation(char* str){
	if(str == NULL) return;
	AllRange2(str, 0, strlen(str));
}

「下一个排列数」的非递归解法

非递归实现最为关键的一部分就是确定下一个排列数。基本思路是：先找到全排列中字典序最小的一个排列，然后找到字典序只比当前排列大的下一个排列，依次查找下去，直到没有新的排列大于当前排列。

对数组进行升序排序，得到全排列中字典序最小的一个排列。
从排列的右端开始，找出第一个比右边数字小的数字的序号，即满足 a[i] > a[i-1]。那么，a[i-1] 右侧的元素降序排列，而且没有比它更大的排列数了。因此，需要调整右侧（包括 a[i-1] 在内）的序列。
为了找到仅比这一序列大 1 的下一序列，将 a[i-1] 和 a[i-1] 右侧所有元素中满足条件 a[j] > a[i-1] 的最小的那个元素交换。交换 a[i-1] 和 a[j]，其中 $j=\min_k \{a_k > a_{i-1}\}$。那么 i-1 位置的元素已经确定。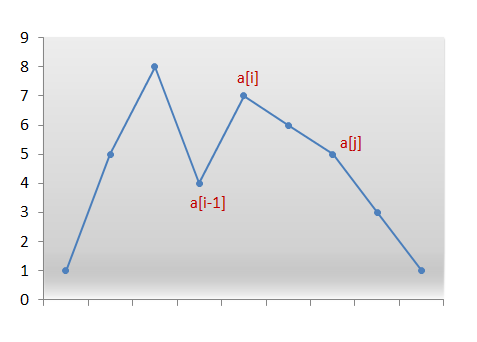
接下来，将 a[i-1] 右侧的序列反转，使其成为升序序列（注意：交换 a[i-1] 和 a[j] 不会改变其原先的降序性质）。这是它们的最小排列。

以上这4步，可以归纳为：一找、二找、三交换、四翻转。

下面的动画可以更清楚地表示这一过程。

非递归方法的时间复杂度是 $O(n)$。在最坏情况下，只需进行两次数组扫描即可。空间复杂度是 $O(1)$，因为无需额外空间，只需进行原地交换。

public class Solution {
    public void nextPermutation(int[] nums) {
        int i = nums.length - 2;
        while (i >= 0 && nums[i + 1] <= nums[i]) {
            i--;
        }
        if (i >= 0) {
            int j = nums.length - 1;
            while (j >= 0 && nums[j] <= nums[i]) {
                j--;
            }
            swap(nums, i, j);
        }
        reverse(nums, i + 1);
    }

    private void reverse(int[] nums, int start) {
        int i = start, j = nums.length - 1;
        while (i < j) {
            swap(nums, i, j);
            i++;
            j--;
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

参考阅读

这篇文章说明了非递归实现的算法的正确性。