[LC21/23] Merge k Sorted Lists / 分治

发表于 | 分类于 ，

本篇梳理「归并多个有序列表」问题。求和问题是指一类从数组中找出 K 个数满足其和为给定整数的问题。

21 Merge 2 Sorted Lits

Merge Two Sorted Lists - LeetCode

Merge two sorted linked lists and return it as a new list. The new list should be made by splicing together the nodes of the first two lists.

显然，可以通过两个指针分别指向链表头，依次比较并移动指针来实现归并。这是一种基本思路，实现起来容易但有点繁琐。

用递归方法解决

递归方法写出的代码就简洁多了。递归终止条件是 「l1 == null 或者 l2 == null」，其他情况只需将递归比较所返回的结果置为 [l1|l2].next 即可。

这种实现并不是尾递归，因此当链表规模过大的时候可能导致「栈溢出」。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    ListNode *mergeTwoLists(ListNode *l1, ListNode *l2) {
        if(l1 == NULL) return l2;
        if(l2 == NULL) return l1;
        
        if(l1->val < l2->val) {
            l1->next = mergeTwoLists(l1->next, l2);
            return l1;
        } else {
            l2->next = mergeTwoLists(l2->next, l1);
            return l2;
        }
    }
};

23 Merge k Sorted Lists

Merge k Sorted Lists - LeetCode

解法1 Brute Force

Brute Force 方法通过遍历 $k$ 个列表的所有数字并排序来完成合并。时间复杂度是 $O(N \log{N})$；空间复杂度是 $O(N)$。其中，$N$ 是所有节点的数目。

解法2 在 $k$ 个数中找到最小数

直接搜索

对于 $k$ 个链表的首位数字，找出它们中的最小数；将该最小数附加到最终形成的链表后面，并将所在位置向后移一位。

时间复杂度是 $O(kN)$；空间复杂度是 $O(N)$。

使用优先队列

将方法 2 中的 $k$ 个首位数字放到优先队列中。这样，每次 “pop” 和 “insert” 操作所需时间是 $O(\log{k})$；而「确定最小数」所需时间是 $O(1)$，因为这个树就是优先队列中的第一个数字。

解法3 合并两个链表

迭代地依次合并两个链表

重复 $k-1$ 次「合并两个链表」的操作。

时间复杂度的计算公式是 $O \left ( \displaystyle\sum_{i=1}^{k-1} \left ( i * \frac{N}{k} + \frac{N}{k} \right ) \right) = O(kN)$。

分治合并

上述方法对于已经完成合并的链表中的元素，进行了多次（重复的）比较。分治方法减少比较的次数。

  1. 将每对链表合并；
  2. 第一次配对后，$k$ 个链表被合并为 $k/2$ 个长度为 $2N/k$ 的链表。接下来，$k/4$，$k/8$……
  3. 重复这个过程直到得到合并后的唯一链表。

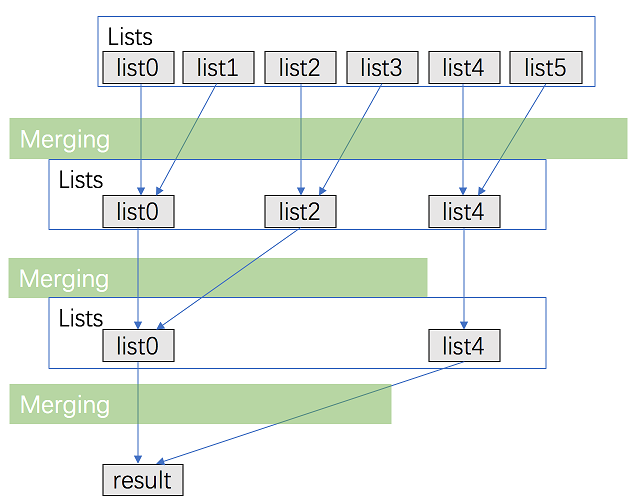
分治方法将时间复杂度减小到 $O(N \log{k})$。