[LC14] Longest Common Prefix / 二分查找 / 分治

发表于 | 分类于 ，

Longest Common Prefix - LeetCode

Write a function to find the longest common prefix string amongst an array of strings.

这道题标签是Easy，也很容易就AC了，但看了一眼解答发现题虽简单，方法却是多种多样，几乎是把好几种经典算法都用上了。虽然时间复杂度没有什么区别和提升，但通过这道题能够复习一下这些经典方法也很值得。

1 水平扫描

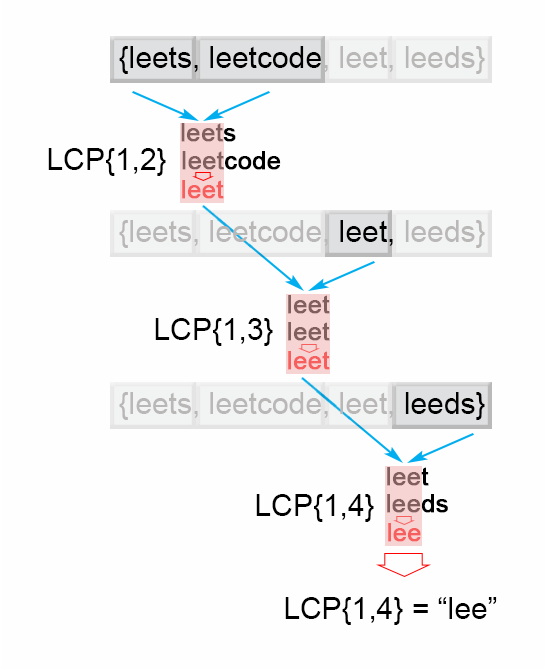
对于一组字符串的「最长公共前缀」（以下用 “LCP” 表示），可以发现：
$$
LCP(s_1, \ldots, s_n) = LCP(LCP(LCP(s_1, s_2), s_3), \ldots, s_n)
$$

算法由内而外、迭代地算出每两个字符串的LCP，从$LCP(s_1, s_2)$开始……在第$n$词迭代完成后，将得到$LCP(s_1, \ldots, s_n)$。若其中有一个字符串为空，算法结束。以下是算法的图示。

1
2
3
4
5
6
7
8
9
10
public String longestCommonPrefix(String[] strs) {
    if (strs.length == 0) return "";
    String prefix = strs[0];
    for (int i = 1; i < strs.length; i++)
        while (strs[i].indexOf(prefix) != 0) {
            prefix = prefix.substring(0, prefix.length() - 1);
            if (prefix.isEmpty()) return "";
        }        
    return prefix;
}

该算法时间复杂度是$O(S)$，其中$S$是所有字符串字符数的总和；空间复杂度是$O(1)$。

2 垂直扫描

如果一个（很）短的字符串排在字符串数组的最后，那么水平扫描仍会做$S$次比较。垂直扫描在每一列（即字符串的每个索引位置）自上到下地扫描，依次比较，然后再扫描下一列……

1
2
3
4
5
6
7
8
9
10
11
public String longestCommonPrefix(String[] strs) {
    if (strs == null || strs.length == 0) return "";
    for (int i = 0; i < strs[0].length() ; i++){
        char c = strs[0].charAt(i);
        for (int j = 1; j < strs.length; j ++) {
            if (i == strs[j].length() || strs[j].charAt(i) != c)
                return strs[0].substring(0, i);             
        }
    }
    return strs[0];
}

该算法时间复杂度是 $O(S)$；空间复杂度是 $O(1)$。注意，与「水平扫描」一致的是，两种算法最坏情况都是当 $n$ 个字符串长度相同（为 $m$）时，都需执行 $S=m \times n$ 次比较。最好情况是只执行 $n \times minLen$ 次比较。

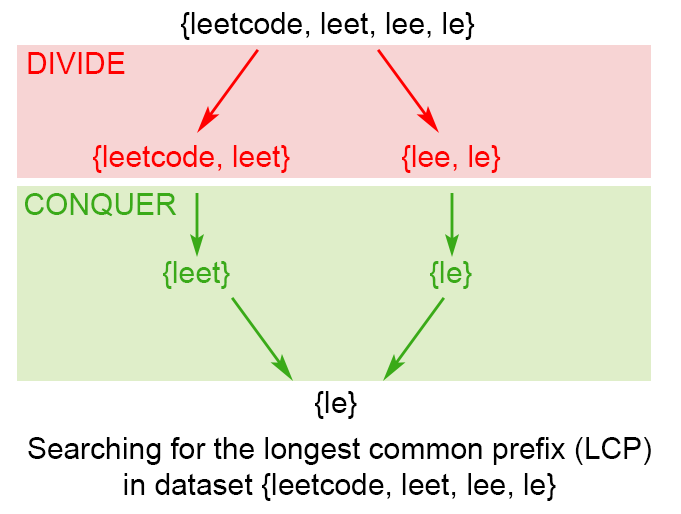
3 分治

分治法将大问题分解为子问题，基于事实：
$$
LCP(s_1, \ldots, s_n) = LCP(LCP(s_1, \ldots, s_k), LCP(s_{k+1}, \ldots, s_n))
$$

只需要递归地分别求取 $LCP(s_1, \ldots, s_k)$ 和 $LCP(s_{k+1}, \ldots, s_n)$，比较两个求得的结果（字符串）得出公共前缀。使用分治法时，$k = mid = \frac{i+j}{2}$。注意，其中的 基础情况 是：当 leftIndex == rightIndex 时，直接返回任一字符串。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public String longestCommonPrefix(String[] strs) {
    if (strs == null || strs.length == 0) return "";    
        return longestCommonPrefix(strs, 0 , strs.length - 1);
}
longestCommonPrefix(String[] strs, int l, int r) {
    if (l == r) {
        return strs[l];
    }
    else {
        int mid = (l + r)/2;
        String lcpLeft =   longestCommonPrefix(strs, l , mid);
        String lcpRight =  longestCommonPrefix(strs, mid + 1,r);
        return commonPrefix(lcpLeft, lcpRight);
   }
}

String commonPrefix(String left,String right) {
    int min = Math.min(left.length(), right.length());       
    for (int i = 0; i < min; i++) {
        if ( left.charAt(i) != right.charAt(i) )
            return left.substring(0, i);
    }
    return left.substring(0, min);
}

算法时间复杂度是$O(S)$，即 $T(n) = 2T(\frac{T}{2}) + O(m)$。最好情况同「垂直扫描」，为 $O(n \times minLen)$。空间复杂度是 $O(m \times \log{n})$，由于在递归调用时占用栈空间，每次需要 $m$ 个字节。

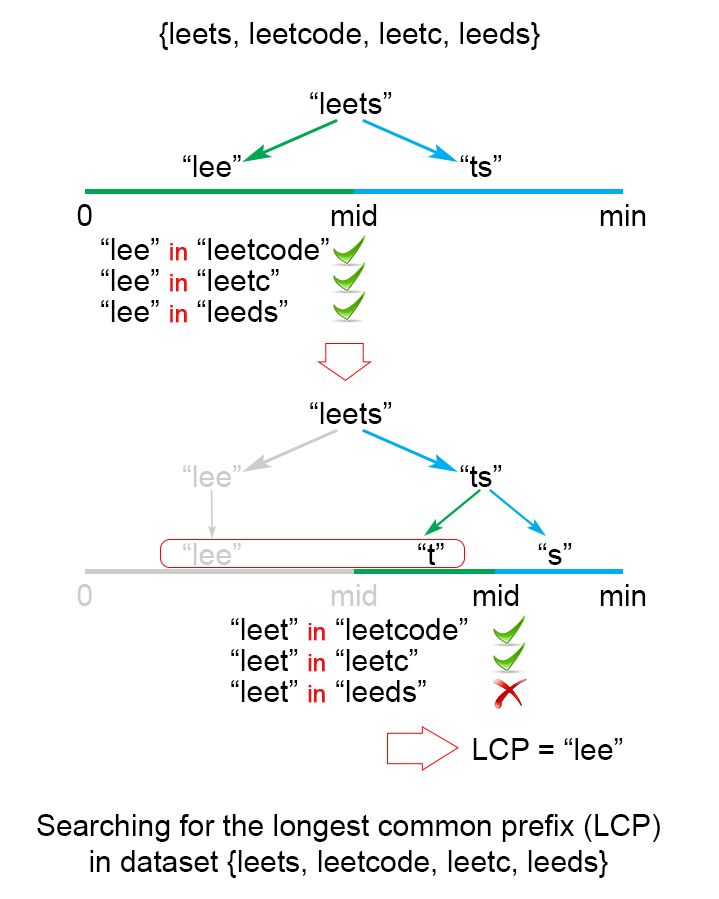
4 二分查找

应用二分查找之前，先确定最短字符串的长度 $minLen$，并将二分查找范围限定在 $(0, minLen)$ 之间。每一次查找都将区间划分为两部分，比较确定 LCP 的长度在其中一个区间，并 丢弃 另一半区间。比较过程不再赘述。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public String longestCommonPrefix(String[] strs) {
    if (strs == null || strs.length == 0)
        return "";
    int minLen = Integer.MAX_VALUE;
    for (String str : strs)
        minLen = Math.min(minLen, str.length());
    int low = 1;
    int high = minLen;
    while (low <= high) {
        int middle = (low + high) / 2;
        if (isCommonPrefix(strs, middle))
            low = middle + 1;
        else
            high = middle - 1;
    }
    return strs[0].substring(0, (low + high) / 2);
}

private boolean isCommonPrefix(String[] strs, int len){
    String str1 = strs[0].substring(0,len);
    for (int i = 1; i < strs.length; i++)
        if (!strs[i].startsWith(str1))
            return false;
    return true;
}

算法时间复杂度是 $O(S \times \log{n})：共执行 $\log{n}} 次迭代，每次迭代执行 $S = m \times n$ 次字符比较。空间复杂度是 $O(1)$。

LeetCode 给出的解答 还考虑了 Trie 树的使用。