[LC10] Regular Expression Matching / 递归 / 动态规划

发表于 | 分类于 ，

Regular Expression Matching - LeetCode

Implement regular expression matching with support for '.' and '*'.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
'.' Matches any single character.
'*' Matches zero or more of the preceding element.

The matching should cover the entire input string (not partial).

The function prototype should be:
bool isMatch(const char *s, const char *p)

Some examples:
isMatch("aa","a") → false
isMatch("aa","aa") → true
isMatch("aaa","aa") → false
isMatch("aa", "a*") → true
isMatch("aa", ".*") → true
isMatch("ab", ".*") → true
isMatch("aab", "c*a*b") → true

1. 用递归解决

我的思路

记得大二的时候高级程序设计做过一次这样的作业。当时做了好久没做出来，后来看了答案才一知半解。主要原因是对「递归」方法掌握得不好，不知道如何使用好递归。

事实上这次也是提交了好多次才通过，不过看到答案给出递归和动态规划两种解决方法，觉得这道题很有参考价值。

我的思路是这样的，在函数体内，分别考虑 p 不同长度对应的比较依据。比较时只考虑 p 的前1位或前2位（如果第2位是'*'），其他情况调用递归函数来比较。

  1. p 长度为0时，只有 s.length() == 0 才成立；
  2. p 长度为1时，要么 p == '.'，要么p == s；
  3. p 长度大于1时，加入对 '*' 的考虑：
    1. 如果第2位是'*'，那么需要比较p和s的第1位（注意排除s长度为0的情况），如果一致还需截断s的第1位再比较第2位……循环结构的停止条件是“不再匹配或s长度为0”。
    2. 如果第2位不是'*'，那么直接比较p和s的第1位并调用递归函数比较字符串剩余部分即可。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public boolean isMatch(String s, String p) {
    if (p.length() == 0) {
        return s.length() == 0;
    }
    if (p.length() == 1) {
        return s.length() == 1 && (p.charAt(0) == '.' || p.charAt(0) == s.charAt(0));
    }
    if (p.charAt(1) != '*') {
        return s.length() != 0 && (p.charAt(0) == '.' || p.charAt(0) == s.charAt(0)) && isMatch(s.substring(1), p.substring(1));
    }
    else {
        while (s.length() != 0 && (p.charAt(0) == '.' || p.charAt(0) == s.charAt(0))) {
            if (isMatch(s, p.substring(2))) {
                return true;
            }
            else {
                s = s.substring(1);
            }
        }
        return isMatch(s, p.substring(2));
    }
}

使用递归的代码效率通常有些低，只超过 7.27%。

2. 递归：语句精炼之道

LeetCode 提供的参考解答所提供的第一个方法就是递归。相比于我的代码，其中简化了许多冗余的语句，代码逻辑更加简洁清晰，值得参考。

1
2
3
4
5
6
7
8
9
10
11
12
public boolean isMatch(String s, String p) {
    if (p.isEmpty()) return s.isEmpty();
    boolean first_match = (!s.isEmpty() &&
            (p.charAt(0) == s.charAt(0) || p.charAt(0) == '.'));

    if (p.length() >= 2 && p.charAt(1) == '*'){
        return (isMatch(s, p.substring(2)) ||
                (first_match && isMatch(s.substring(1), p)));
    } else {
        return first_match && isMatch(s.substring(1), p.substring(1));
    }
}

注意 return (isMatch(s, p.substring(2)) || (first_match && isMatch(s.substring(1), p))); 中「或」关系前后的两个递归判断综合计算了通配符 '*' 出现时用于于「0 次」与「多次」的两种情形。

其依据是：通配符 '*' 只能出现在 p 的第二个位置，我们考虑直接 忽略这个部分（代表前置字符出现 0 次），或者当 s 中第 1 个字符已匹配时递归地判断后面的。s 和 p 的剩余部分仍然匹配的（递归匹配），则认为原始字符串匹配，比如 'ba*' 可以对应 'b', 'ba', 'baa', ...。

3. 动态规划

求解公式和表格

理解了递归方法后，动态规划中的大部分逻辑也就随之得到了。但动态规划的优势是能够在 $O(n^2)$ 的时间复杂度内解决问题；相比之下，递归方法的时间复杂度是 $O((T+P)2^{T+\frac{P}{2}})$（分析参考 LeetCode 的解答）

此问题的递归公式由一个二维表格求解。二维表格大小是string.length + 1 $\times$ pattern.length + 1。其中第 $i$ 行第 $j$ 列表示的含义是：string[1..i] 和 pattern[1..j] 是否匹配。 求解公式是：

$$
T[i][j] = \begin{cases}
T[i-1][j-1] & \text{ if s[i] == p[j] or p[j] == ‘.’} \\
T[i][j-2] & \text{ if p[j] == ‘*‘} \\
T[i-1][j] & \text{ if p[j] == ‘*‘ and (s[i] == p[j-1] or p[j-1] == ‘.’)} \\
\text{false} & \text{ otherwise }
\end{cases}
$$

下图是以 s = "xaabyc" 和 p = "xa*b.c" 例子所对应的 DP 表格。尝试在绘制表格的过程中总结出求解公式，思考计算每个值的时候如何根据已计算的值推算。

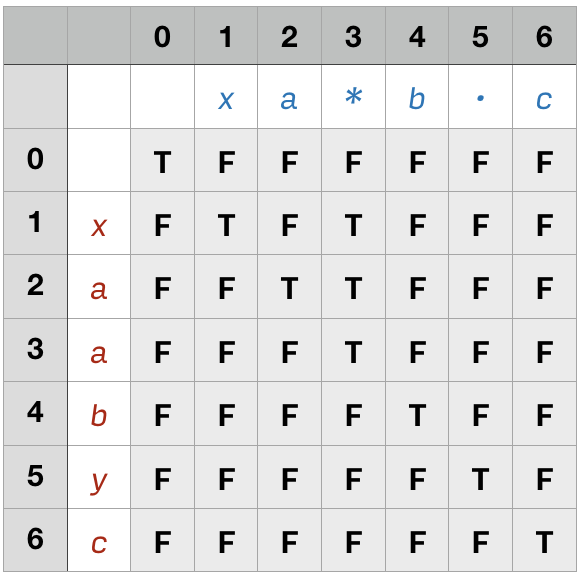
表格中第 0 列均为 False，但第 0 行是不一定均为 False 的，因为空串与"a*b*"也是匹配的！

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public boolean matchRegex(char[] text, char[] pattern) {
    boolean T[][] = new boolean[text.length + 1][pattern.length + 1];

    T[0][0] = true;
    //Deals with patterns like a* or a*b* or a*b*c*
    for (int i = 1; i < T[0].length; i++) {
        if (pattern[i-1] == '*') {
            T[0][i] = T[0][i - 2];
        }
    }

    for (int i = 1; i < T.length; i++) {
        for (int j = 1; j < T[0].length; j++) {
            if (pattern[j - 1] == '.' || pattern[j - 1] == text[i - 1]) {
                T[i][j] = T[i-1][j-1];
            } else if (pattern[j - 1] == '*')  {
                T[i][j] = T[i][j - 2];
                if (pattern[j-2] == '.' || pattern[j - 2] == text[i - 1]) {
                    T[i][j] = T[i][j] | T[i - 1][j];
                }
            } else {
                T[i][j] = false;
            }
        }
    }
    return T[text.length][pattern.length];
}

动态规划部分的实现和代码来源于 https://youtu.be/l3hda49XcDE。

总结

如何写出DP表达式？

  1. 确定问题子结构。
  2. 可以先根据一个简单例子试着画表格，在画表格的过程中仔细考虑填写每一项可以由已求得结果（表格中已填项）得到什么信息。