[LC5/9] Palindrome Problems / 动态规划

发表于 | 分类于 ，

第5题和第9题都与「回文字符串」有关，且用到了经典的「动态规划」方法。在「最长回文串」问题中，Manacher 算法是一种技巧性极高的经典方法。

9 Palindrome Number

Palindrome Number - LeetCode

Determine whether an integer is a palindrome. Do this without extra space.

直觉上的解法 [AC]

为了判定整数是不是 回文数，且不能将其转换为字符串处理，直觉是通过循环，在每一轮取整数的最低位和最高位比较（如对于1221取两个1进行比较），下一轮分别向右向左移一位……直到每两个数字都相等，该整数就是回文数。

由该思路直接写成的代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class Solution {
    public boolean isPalindrome(int x) {
        if (x < 0) {
            return false;
        }
        int left_div = 1;
        int right_div = 10;
        while (x / left_div >= 10) {
            left_div *= 10;
        }
        while (left_div >= right_div) {
            int l = x / left_div % 10;
            int r = (x % right_div) / (right_div / 10);
            if (l != r) {
                return false;
            }
            left_div /= 10;
            right_div *= 10;
        }
        return true;
    }
}

另一种方法：翻转数字「一半」

LeetCode 解答 给出了这种方法的描述。

For number 1221, if we do 1221 % 10, we get the last digit 1, to get the second to the last digit, we need to remove the last digit from 1221, we could do so by dividing it by 10, 1221 / 10 = 122. Then we can get the last digit again by doing a modulus by 10, 122 % 10 = 2, and if we multiply the last digit by 10 and add the second last digit, 1 * 10 + 2 = 12, it gives us the reverted number we want. Continuing this process would give us the reverted number with more digits.

Since we divided the number by 10, and multiplied the reversed number by 10, when the original number is less than the reversed number, it means we’ve processed half of the number digits.

简而言之，就是不断地对原数x不断除以10，并在得到结果同时计算 当前 的revertedNumber，直至 x < revertedNumber。需要额外考虑的是，如果x有奇数个数字，如12321，x和revertedNumber在比较时分别是什么？

完整过程如下。

1
2
3
4
5
6
7
8
9
10
11
12
public bool IsPalindrome(int x) {
    if(x < 0 || (x % 10 == 0 && x != 0)) {
        return false;
    }

    int revertedNumber = 0;
    while(x > revertedNumber) {
        revertedNumber = revertedNumber * 10 + x % 10;
        x /= 10;
    }
    return x == revertedNumber || x == revertedNumber/10;
}

5 Longest Palindromic Substring

Longest Palindromic Substring - LeetCode

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

1
2
3
Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

Brute Force [TLE]

直接求解该问题根据每个起始点、终点在原字符串中截取子字符串（时间复杂度为$O(n^2)$），并且通过$O(n)$时间检查是否为回文串。总时间复杂度为$O(n^3)$，空间复杂度为$O(1)$。

动态规划方法

方法描述

动态规划方法可以避免重复计算（利用已经计算的结果）。在本题中，可以再验证回文串时使用已经计算的结果（检验结果）。考虑字符串"ababa"，如果我们已知"bab"为回文串，那么"ababa"也肯定是回文串，因为它是在回文串"bab"首尾各加一个相同的字符构造出来的。

按以下方式定义动态规划表格中的项P[i,j]：

$$
P[i,j] =
\begin{cases}
\text{true} & \text{ if the substring } S_i \ldots S_j \text{ is a palindrome } \\
\text{false} & \text{ otherwise }
\end{cases}
$$

即 $P[i,j] = (P[i+1, j-1] \text{ and } S_i == S_j)$

在填充动态规划表格的第一步和第二步，分别执行：

  1. $P[i, j] = $ true
  2. $P[i, i + 1] = (S_i == S_j)$

总体思路是，先初始化长度为1和2的回文串（所对应的数据表项），然后确定长度为3的回文串（所对应的数据表项），然后……

这样就实现了一个时间复杂度和空间复杂度均为 $O(n^2)$ 的动态规划方法。

代码实现

在实现时，考虑如何绘制动态规划表格：

  1. 动态规划表格 的第一维是指子字符串起始位置，第二维是指终止位置，所存布尔型数据表示是否回文；
  2. 两层循环并非从左到右依次填表。外循环的变量i控制 字符串首到尾的增量（子串长度），内循环变量j表示开始分析子串的起始位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public String longestPalindrome(String s) {
    int len = s.length();
    boolean[][] dp = new boolean[len][len];
    int maxLen = 0;
    int startIdx = 0;

    for (int i = 0; i < len; i++) {
        for (int j = 0; j < len - i; j++) {
            if (i == 0 || i == 1 && s.charAt(j) == s.charAt(j+1)) {
                dp[j][j+i] = true;
            }
            else if (s.charAt(j) == s.charAt(j+i)) {
                dp[j][j+i] = dp[j+1][j+i-1];
            }
            if (dp[j][j+i] && i + 1 > maxLen) {
                maxLen = i + 1;
                startIdx = j;
            }
        }
    }
    return s.substring(startIdx, startIdx + maxLen);
}

考虑：如何进一步减小空间复杂度？下一节介绍空间复杂度为 $O(1)$ 的方法。

中心扩散法（Expand Around Center）

中心扩散法用 $O(n)$ 的时间和 $O(1)$ 的空间解决问题。

该方法基于一个事实，即 任何回文串以其中心点左右对称。也可以说，回文串可以从中心点向外扩散（构造出来）。中心点有 $2n-1$ 个可能位置（考虑中心点在两个字符之间的情况）。

所以如果我们从小到大依次对以某点为中心的所有子字符串进行计算，就能省略存放所有子字符串的回文情况的空间（一个二维数组）。这种解法中，外层循环遍历的是 子字符串的中心点，内层循环则是从中心 扩散，一旦不是回文就不再计算其他以此为中心的较大的字符串。由于中心对称有 两种情况，一是奇数个字母以某个字母对称，二是偶数个字母以两个字母中间为对称，要分别计算这两种对称情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public String longestPalindrome(String s) {
    int start = 0, end = 0;
    for (int i = 0; i < s.length(); i++) {
        int len1 = expandAroundCenter(s, i, i);
        int len2 = expandAroundCenter(s, i, i + 1);
        int len = Math.max(len1, len2);
        if (len > end - start) {
            start = i - (len - 1) / 2;
            end = i + len / 2;
        }
    }
    return s.substring(start, end + 1);
}

private int expandAroundCenter(String s, int left, int right) {
    int L = left, R = right;
    while (L >= 0 && R < s.length() && s.charAt(L) == s.charAt(R)) {
        L--;
        R++;
    }
    return R - L - 1;
}

Manacher 算法

关于这个算法找了很多资料学习，发现了一篇比较好的文章。将其摘录下来。

先来看看中心扩散法存在的缺陷。

  1. 由于回文串长度的奇偶性造成了不同性质的对称轴位置，算法要对两种情况分别处理；

  2. 很多子串被重复多次访问，造成较差的时间效率。例如：

    1
    2
    char: a b a b a
      i : 0 1 2 3 4

    当i==1和i==2时，左边的子串aba分别被遍历了一次。

Manacher正是针对这些问题改进算法。

解决长度奇偶性带来的对称轴位置问题

Manacher算法首先对字符串做一个预处理，在所有的空隙位置(包括首尾)插入同样的符号，要求这个符号是不会在原串中出现的。这样会使得所有的串都是奇数长度的。以插入#号为例：

1
2
aba  ———>  #a#b#a#
abba ———>  #a#b#b#a#

插入的是同样的符号，且符号不存在于原串，因此子串的回文性不受影响，原来是回文的串，插完之后还是回文的，原来不是回文的，依然不会是回文。

解决重复访问的问题

我们把一个回文串中最左或最右位置的字符与其对称轴的距离称为回文半径。Manacher定义了一个回文半径数组RL，用RL[i]表示以第i个字符为对称轴的回文串的回文半径。我们一般对字符串从左往右处理，因此这里定义RL[i]为第i个字符为对称轴的回文串的最右一个字符与字符i的距离。对于上面插入分隔符之后的两个串，可以得到RL数组：

1
2
3
4
5
6
7
8
9
char:    # a # b # a #
 RL :    1 2 1 4 1 2 1
RL-1:    0 1 0 3 0 1 0
  i :    0 1 2 3 4 5 6

char:    # a # b # b # a #
 RL :    1 2 1 2 5 2 1 2 1
RL-1:    0 1 0 1 4 1 0 1 0
  i :    0 1 2 3 4 5 6 7 8

上面我们还求了一下RL[i]-1。通过观察可以发现，RL[i]-1的值，正是在原本那个没有插入过分隔符的串中，以位置i为对称轴的最长回文串的长度。那么只要我们求出了RL数组，就能得到最长回文子串的长度。

于是问题变成了，怎样高效地求的RL数组。基本思路是 利用回文串的对称性，扩展回文串。

我们再引入一个辅助变量MaxRight，表示当前访问到的所有回文子串，所能触及的最右一个字符的位置。另外还要记录下MaxRight对应的回文串的对称轴所在的位置，记为pos，它们的位置关系如下。

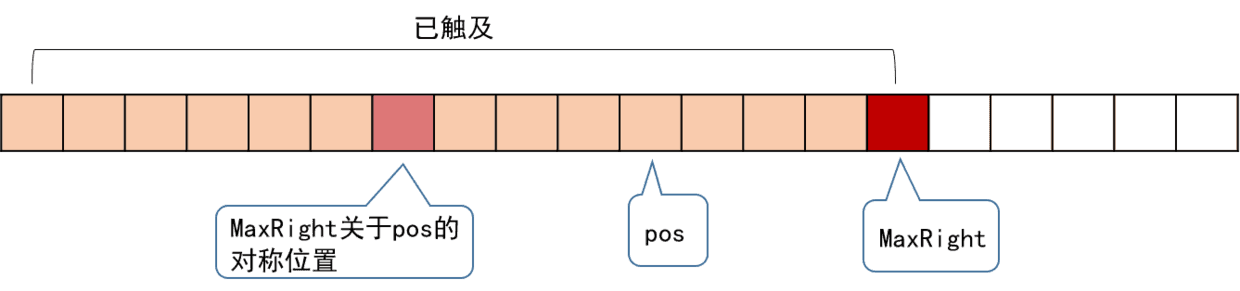
我们从左往右地访问字符串来求RL，假设当前访问到的位置为i，即要求RL[i]，在对应上图，i必然是在pos右边的。但我们更关注的是，i是在MaxRight的左边还是右边。我们分情况来讨论。

1) 当i在MaxRight的左边

情况1)可以用下图来刻画：

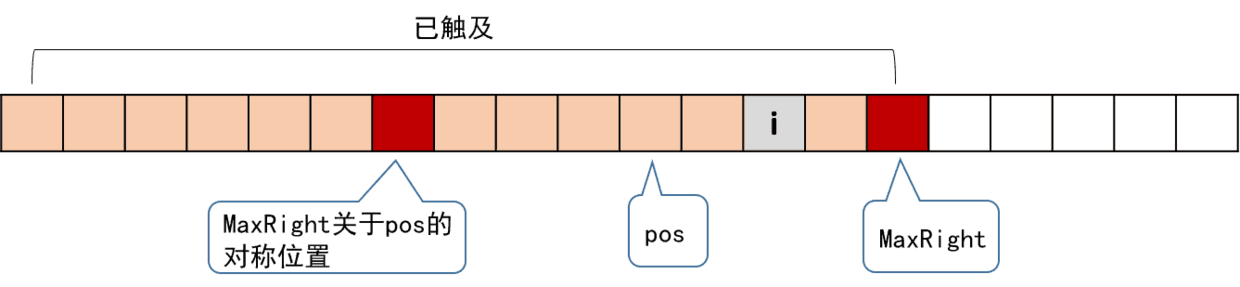
我们知道，图中两个红色块之间（包括红色块）的串是回文的；并且以i为对称轴的回文串，是与红色块间的回文串有所重叠的。我们找到i关于pos的对称位置j，这个j对应的RL[j]我们是已经算过的。根据回文串的对称性，以i为对称轴的回文串和以j为对称轴的回文串，有一部分是相同的。这里又有两种细分的情况。

  1. 以j为对称轴的回文串比较短，短到像下图这样。

    这时我们知道RL[i]至少不会小于RL[j]，并且已经知道了部分的以i为中心的回文串，于是可以令RL[i]=RL[j]。但是以i为对称轴的回文串可能实际上更长，因此我们试着以i为对称轴，继续往左右两边扩展，直到左右两边字符不同，或者到达边界。

  2. 以j为对称轴的回文串很长，这么长：（此处蓝线位置有误——注）

    这时，我们只能确定，两条蓝线之间的部分（即不超过MaxRight的部分）是回文的，于是从这个长度开始，尝试以i为中心向左右两边扩展，，直到左右两边字符不同，或者到达边界。

不论以上哪种情况，之后都要尝试更新MaxRight和pos，因为有可能得到更大的MaxRight。

具体操作如下：

1
2
3
step 1: 令RL[i]=min(RL[2*pos-i], MaxRight-i)
step 2: 以i为中心扩展回文串，直到左右两边字符不同，或者到达边界。
step 3: 更新MaxRight和pos

2) 当i在MaxRight的右边

遇到这种情况，说明以i为对称轴的回文串还没有任何一个部分被访问过，于是只能从i的左右两边开始尝试扩展了，当左右两边字符不同，或者到达字符串边界时停止。然后更新MaxRight和pos。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#Python
def manacher(s):
    #预处理
    s='#'+'#'.join(s)+'#'

    RL=[0]*len(s)
    MaxRight=0
    pos=0
    MaxLen=0
    for i in range(len(s)):
        if i<MaxRight:
            RL[i]=min(RL[2*pos-i], MaxRight-i)
        else:
            RL[i]=1
        #尝试扩展，注意处理边界
        while i-RL[i]>=0 and i+RL[i]<len(s) and s[i-RL[i]]==s[i+RL[i]]:
            RL[i]+=1
        #更新MaxRight,pos
        if RL[i]+i-1>MaxRight:
            MaxRight=RL[i]+i-1
            pos=i
        #更新最长回文串的长度
        MaxLen=max(MaxLen, RL[i])
    return MaxLen-1

相关问题：Longest Palindromic Subsequence

最长回文子序列与子串的区别在于：回文序列中，每个字符不一定是连续出现的。

使用动态规划方法。动态规划表格中的每一项T[i, j]表示 以i为起始点、j为终点的子串中最长回文子序列的长度。其计算公式为：

$$
T[i, j] = \begin{cases}
T[i + 1, j - 1] + 2 & \text{ if input[i] == input[j]} \\
{\rm max}(T[i + 1, j], T[i, j-1]) & \text{ otherwise }
\end{cases}
$$

以上来源于 Tushar Roy 的讲解视频。

参考资料